How to R - Guide du débutant Analyse des séries temporelles
- Science des données
- beginners guide, forecast, r, time series
- 5 min de lecture
Dr. Stefan Lieder
Le guide "How to R - Beginner Guide Time Series Analysis" présente une analyse de séries temporelles avec R, en esquissant les principales étapes de la préparation des données, de la modélisation et de la visualisation. L'utilisation des packs R tidyverse, tsibble et fable est mise en avant.
Table des matières
Analyse de séries temporelles avec R
Nous nous limiterons dans ce petit tutoriel à esquisser brièvement les étapes essentielles de l'analyse des séries temporelles dans le langage de programmation R.
Il s'agit de
- Préparation des données,
- Modélisation et
- Visualisation.
Nous utilisons pour cela les paquets R tidyverse, tsibble et fable.
Préparation des données
En règle générale, toutes les fonctions nécessaires à la préparation générale des données sont contenues dans le paquet "tidyverse". Pour la préparation des données dans le style "tidy", le paquet "tsibble" est toutefois également nécessaire. Tout d'abord, nous chargeons les paquets et les données :
library(fable)
library(tsibble)
library(tidyverse, quietly = TRUE, warn.conflicts = FALSE)
raw_data = read_delim("~/Documents/Progonosewerkstatt/Peer_Labs/R/2_DataPreparation/01_Data/Company.csv", delim=";")
glimpse(raw_data)
## Rows: 101
## Columns: 9
## $ Month <dttm> 2011-01-01, 2011-02-01, 2011-03-01, 2011-04-01, 2011-05-…
## $ Germany <dbl> 19722000, 25062000, 47066000, 52625000, 66489000, 5660100…
## $ Canada <dbl> 1809000, 2206000, 3035000, 3793000, 4813000, 4370000, 454…
## $ Switzerland <dbl> 3624000, 4972000, 7010000, 7084000, 9452000, 7971000, 733…
## $ Austria <dbl> 1436000, 2390000, 6556000, 7544000, 9069000, 8154000, 817…
## $ US <dbl> 3598000, 3349000, 6101000, 6098000, 6935000, 8644000, 757…
## $ France <dbl> 4861000, 5465000, 8440000, 8223000, 9706000, 8809000, 806…
## $ Sweden <dbl> 10723000, 12333000, 23562000, 30595000, 46253000, 3886900…
## $ China <dbl> 8103000, 4040000, 25974000, 34776000, 31125000, 31576000,…
Im “tidy”-Style werden die Daten im Long-Format benötigt. Wir nutzen die “pivot_longer” Funktion. Anschliessend konvertieren wir das tibble-Objekt (= tidy dataframe) in ein tsibble Objekt, welches ein dataframe für Zeitreihen ist.
prep_data = raw_data %>%
pivot_longer(., cols = 2:9, names_to = "Subsidiary", values_to = "Revenues") %>%
mutate(Month = yearmonth(Month)) %>%
tsibble(., key = Subsidiary, index = Month)
glimpse(prep_data)
## Rows: 808
## Columns: 3
## Key: Subsidiary [8]
## $ Month <mth> 2011 Jan, 2011 Feb, 2011 Mar, 2011 Apr, 2011 May, 2011 Jun…
## $ Subsidiary <chr> "Austria", "Austria", "Austria", "Austria", "Austria", "Au…
## $ Revenues <dbl> 1436000, 2390000, 6556000, 7544000, 9069000, 8154000, 8173…
Pour avoir une idée des données, commençons par les regarder.
prep_data %>% autoplot(Revenues)
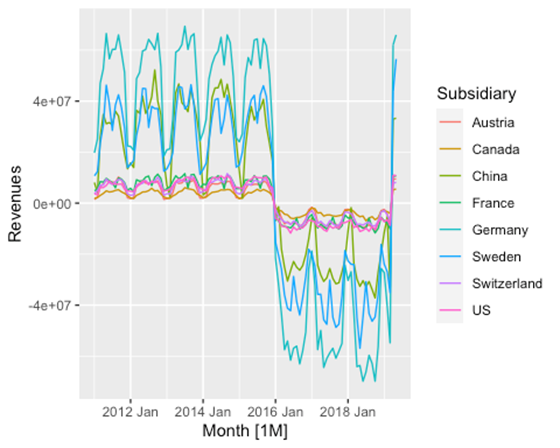
Nous constatons qu'il y a une rupture dans les données entre 2016 et début 2020. Après avoir consulté l'expert technique, nous savons qu'il s'agit d'un changement de système et que toutes les valeurs doivent être non négatives. Nous corrigeons cela.
prep_data = prep_data %>%
mutate(Revenues = abs(Revenues))
prep_data %>% autoplot(Revenues)
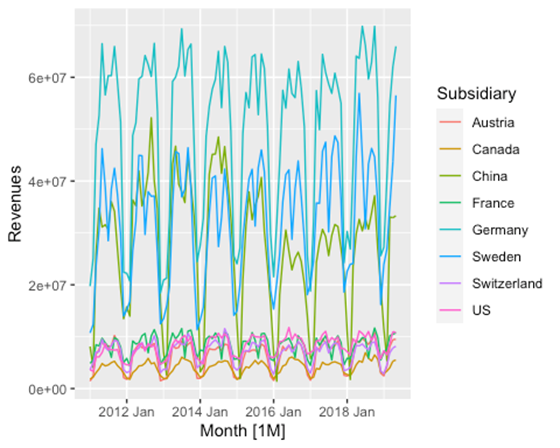
On voit maintenant que les séries chronologiques disponibles ont un fort caractère saisonnier. Les données sont ainsi traitées et peuvent être modélisées.
Modélisation de l'analyse des séries temporelles
Deux modèles très répandus, disponibles dans le package Fable, sont ETS et ARIMA. Ces modèles sont indiqués avec une représentation de formulaire compacte. La variable de réponse (Revenues) et toutes les transformations sont contenues dans le côté gauche, tandis que la spécification du modèle se trouve dans le côté droit de la formule. Si un modèle n'est pas entièrement spécifié (ou si le côté droit de la formule est complètement absent), les composants non spécifiés sont automatiquement sélectionnés.
Nous utilisons les deux classes de modèles pour trouver le meilleur modèle pour chaque série chronologique.
fit <- prep_data %>%
model(
ets = ETS(Revenues),
arima = ARIMA(Revenues)
)
## Warning in sqrt(diag(best$var.coef)): NaNs produced
Avec coef(), on peut accéder à tous les paramètres d'ajustement d'un modèle.
fit %>% coef()
## # A tibble: 145 x 7
## Subsidiary .model term estimate std.error statistic p.value
## <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Austria ets alpha 2.21e-1 NA NA NA
## 2 Austria ets gamma 1.00e-4 NA NA NA
## 3 Austria ets l 6.43e+6 NA NA NA
## 4 Austria ets s0 -4.15e+6 NA NA NA
## 5 Austria ets s1 -3.35e+5 NA NA NA
## 6 Austria ets s2 2.47e+6 NA NA NA
## 7 Austria ets s3 2.42e+6 NA NA NA
## 8 Austria ets s4 1.35e+6 NA NA NA
## 9 Austria ets s5 1.78e+6 NA NA NA
## 10 Austria ets s6 1.82e+6 NA NA NA
## # … with 135 more rows
glance permet de visualiser différentes caractéristiques statistiques de l'adaptation du modèle à la série temporelle.
fit %>% glance
## # A tibble: 16 x 12
## Subsidiary .model sigma2 log_lik AIC AICc BIC MSE AMSE
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Austria ets 3.51e+11 -1568. 3166. 3172. 3205. 3.02e11 3.14e11
## 2 Canada ets 1.08e- 2 -1529. 3088. 3093. 3127. 1.47e11 1.53e11
## 3 China ets 1.84e+13 -1768. 3566. 3572. 3605. 1.59e13 2.76e13
## 4 France ets 5.57e+11 -1591. 3213. 3218. 3252. 4.80e11 4.79e11
## 5 Germany ets 1.98e+13 -1772. 3573. 3579. 3613. 1.71e13 1.73e13
## 6 Sweden ets 1.08e+13 -1741. 3512. 3517. 3551. 9.26e12 1.02e13
## 7 Switzerla… ets 3.61e+11 -1569. 3169. 3175. 3208. 3.11e11 3.20e11
## 8 US ets 5.81e- 3 -1568. 3172. 3181. 3219. 3.20e11 3.23e11
## 9 Austria arima 4.55e+11 -1308. 2624. 2625. 2634. NA NA
## 10 Canada arima 1.82e+11 -1285. 2581. 2582. 2593. NA NA
## 11 China arima 2.07e+13 -1492. 2992. 2992. 3002. NA NA
## 12 France arima 5.13e+11 -1329. 2672. 2674. 2690. NA NA
## 13 Germany arima 2.20e+13 -1498. 3003. 3003. 3010. NA NA
## 14 Sweden arima 1.10e+13 -1468. 2944. 2944. 2954. NA NA
## 15 Switzerla… arima 4.56e+11 -1322. 2655. 2655. 2667. NA NA
## 16 US arima 4.78e+11 -1311. 2633. 2634. 2648. NA NA
## # … with 3 more variables: MAE <dbl>, ar_roots <list>, ma_roots <list>
Avec la fonction Forecast, nous générons les prévisions pour chaque série temporelle à partir des modèles.
fc = fit %>%
forecast(h = "2 years")
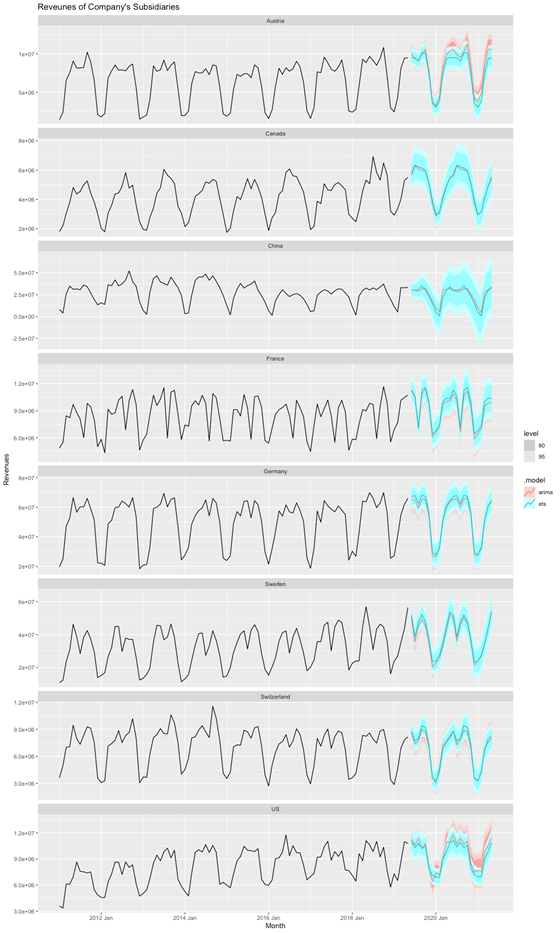
Enfin, nous visualisons les prévisions. On peut voir que les deux méthodes captent les modèles des différentes séries temporelles et les intègrent dans les prévisions de leur méthodologie respective, comme c'est le cas par exemple pour le "creux de l'été" dans la filiale française ou la tendance à la hausse dans la société américaine.
fc %>% autoplot(prep_data) +
ggtitle("Reveunes of Company's Subsidiaries")
Télécharger l'article wiki au format PDF
En savoir plus ?
Vous souhaitez approfondir ce sujet ? Dans ce cas, nous serions ravis de discuter personnellement avec vous des domaines d'application de R - volontiers aussi en relation avec les produits Analytics de SAP. N'hésitez pas à prendre contact avec nous !
