How to R – Beginner Guide Zeitreihenanalyse
- Data Science
- beginners guide, forecast, r, time series
- 5 Min Lesezeit
Dr. Stefan Lieder
In der Anleitung „How to R – Beginner Guide Zeitreihenanalyse“ wird eine Zeitreihenanalyse mit R durchgeführt, wobei die wesentlichen Schritte der Datenaufbereitung, Modellierung und Visualisierung skizziert werden. Die Nutzung der R-Pakete tidyverse, tsibble und fable sehen dabei im Fokus.
Inhaltsverzeichnis
Zeitreihenanalyse mit R
Wir beschränken uns in diesem kleinen Tutorial darauf, die wesentlichen Schritte in der Zeitreihenanalyse kurz in der Programmiersprache R zu skizzieren.
Diese sind:
- Datenaufbereitung,
- Modellierung und
- Visualisierung.
Wir nutzen dafür die R Pakete tidyverse, tsibble und fable.
Datenaufbereitung
In der Regel sind alle nötigen Funktionen zur allgemeinen Datenaufbereitung in der Paketsammlung “tidyverse” enthalten. Für die Datenaufbereitung im “tidy”-Style wird allerdings auch noch das “tsibble” Paket benötigt. Zunächst laden wir die Pakete und die Daten:
library(fable)
library(tsibble)
library(tidyverse, quietly = TRUE, warn.conflicts = FALSE)
raw_data = read_delim("~/Documents/Progonosewerkstatt/Peer_Labs/R/2_DataPreparation/01_Data/Company.csv", delim=";")
glimpse(raw_data)
## Rows: 101
## Columns: 9
## $ Month <dttm> 2011-01-01, 2011-02-01, 2011-03-01, 2011-04-01, 2011-05-…
## $ Germany <dbl> 19722000, 25062000, 47066000, 52625000, 66489000, 5660100…
## $ Canada <dbl> 1809000, 2206000, 3035000, 3793000, 4813000, 4370000, 454…
## $ Switzerland <dbl> 3624000, 4972000, 7010000, 7084000, 9452000, 7971000, 733…
## $ Austria <dbl> 1436000, 2390000, 6556000, 7544000, 9069000, 8154000, 817…
## $ US <dbl> 3598000, 3349000, 6101000, 6098000, 6935000, 8644000, 757…
## $ France <dbl> 4861000, 5465000, 8440000, 8223000, 9706000, 8809000, 806…
## $ Sweden <dbl> 10723000, 12333000, 23562000, 30595000, 46253000, 3886900…
## $ China <dbl> 8103000, 4040000, 25974000, 34776000, 31125000, 31576000,…
Im “tidy”-Style werden die Daten im Long-Format benötigt. Wir nutzen die “pivot_longer” Funktion. Anschliessend konvertieren wir das tibble-Objekt (= tidy dataframe) in ein tsibble Objekt, welches ein dataframe für Zeitreihen ist.
prep_data = raw_data %>%
pivot_longer(., cols = 2:9, names_to = "Subsidiary", values_to = "Revenues") %>%
mutate(Month = yearmonth(Month)) %>%
tsibble(., key = Subsidiary, index = Month)
glimpse(prep_data)
## Rows: 808
## Columns: 3
## Key: Subsidiary [8]
## $ Month <mth> 2011 Jan, 2011 Feb, 2011 Mar, 2011 Apr, 2011 May, 2011 Jun…
## $ Subsidiary <chr> "Austria", "Austria", "Austria", "Austria", "Austria", "Au…
## $ Revenues <dbl> 1436000, 2390000, 6556000, 7544000, 9069000, 8154000, 8173…
Um ein Gefühl für die Daten zu bekommen, schauen wir sie uns zunächst an.
prep_data %>% autoplot(Revenues)
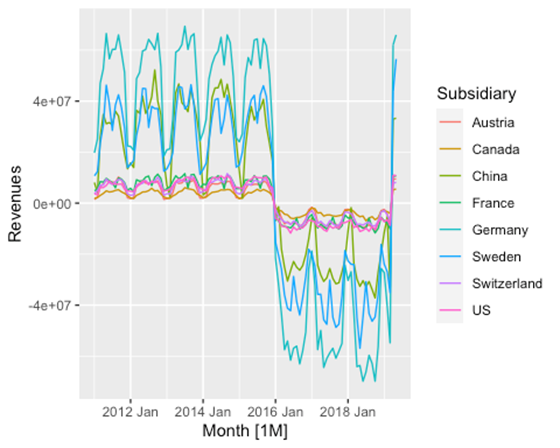
Wir sehen, dass es einen Bruch in den Daten zwischen 2016 und Anfang 2020 gibt. Nach Rücksprache mit dem Fachexperten wissen wir, dass es sich um eine Systemumstellung handelt und alle Werte nicht-negativ sein müssen. Wir korrigieren das.
prep_data = prep_data %>%
mutate(Revenues = abs(Revenues))
prep_data %>% autoplot(Revenues)
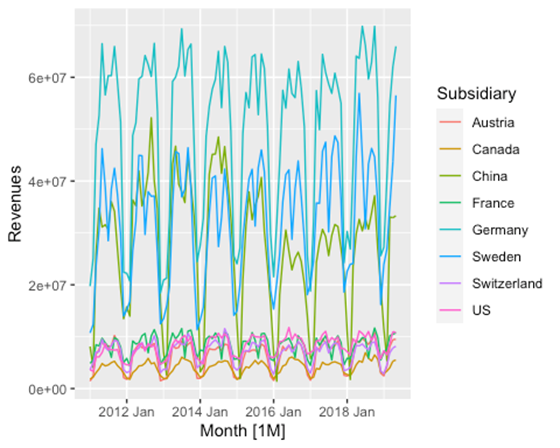
Man sieht nun, dass die vorliegenden Zeitreihen einen starken saisonalen Charakter besitzen. Die Daten sind damit aufbereitet und können modelliert werden.
Modellierung der Zeitreihenanalyse
Zwei weit verbreitete Modelle, die im Fable Paket verfügbar sind, sind ETS und ARIMA. Diese Modelle werden mit einer kompakten Formeldarstellung angegeben. Die Antwortvariable (Revenues) und alle Transformationen sind auf der linken Seite enthalten, während die Modellspezifikation auf der rechten Seite der Formel steht. Wenn ein Modell nicht vollständig spezifiziert ist (oder wenn die rechte Seite der Formel komplett fehlt), werden die nicht-spezifizierten Komponenten automatisch ausgewählt.
Wir verwenden beide Modellklassen, um das beste Modell für die jeweilige Zeitreihe zu finden.
fit <- prep_data %>%
model(
ets = ETS(Revenues),
arima = ARIMA(Revenues)
)
## Warning in sqrt(diag(best$var.coef)): NaNs produced
Mit coef() kann man auf alle Fitparameter eines Modells zugreifen.
fit %>% coef()
## # A tibble: 145 x 7
## Subsidiary .model term estimate std.error statistic p.value
## <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Austria ets alpha 2.21e-1 NA NA NA
## 2 Austria ets gamma 1.00e-4 NA NA NA
## 3 Austria ets l 6.43e+6 NA NA NA
## 4 Austria ets s0 -4.15e+6 NA NA NA
## 5 Austria ets s1 -3.35e+5 NA NA NA
## 6 Austria ets s2 2.47e+6 NA NA NA
## 7 Austria ets s3 2.42e+6 NA NA NA
## 8 Austria ets s4 1.35e+6 NA NA NA
## 9 Austria ets s5 1.78e+6 NA NA NA
## 10 Austria ets s6 1.82e+6 NA NA NA
## # … with 135 more rows
Mit glance können verschiedene statistische Kenngrössen der Anpassung des Modells auf die Zeitreihe eingesehen werden.
fit %>% glance
## # A tibble: 16 x 12
## Subsidiary .model sigma2 log_lik AIC AICc BIC MSE AMSE
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Austria ets 3.51e+11 -1568. 3166. 3172. 3205. 3.02e11 3.14e11
## 2 Canada ets 1.08e- 2 -1529. 3088. 3093. 3127. 1.47e11 1.53e11
## 3 China ets 1.84e+13 -1768. 3566. 3572. 3605. 1.59e13 2.76e13
## 4 France ets 5.57e+11 -1591. 3213. 3218. 3252. 4.80e11 4.79e11
## 5 Germany ets 1.98e+13 -1772. 3573. 3579. 3613. 1.71e13 1.73e13
## 6 Sweden ets 1.08e+13 -1741. 3512. 3517. 3551. 9.26e12 1.02e13
## 7 Switzerla… ets 3.61e+11 -1569. 3169. 3175. 3208. 3.11e11 3.20e11
## 8 US ets 5.81e- 3 -1568. 3172. 3181. 3219. 3.20e11 3.23e11
## 9 Austria arima 4.55e+11 -1308. 2624. 2625. 2634. NA NA
## 10 Canada arima 1.82e+11 -1285. 2581. 2582. 2593. NA NA
## 11 China arima 2.07e+13 -1492. 2992. 2992. 3002. NA NA
## 12 France arima 5.13e+11 -1329. 2672. 2674. 2690. NA NA
## 13 Germany arima 2.20e+13 -1498. 3003. 3003. 3010. NA NA
## 14 Sweden arima 1.10e+13 -1468. 2944. 2944. 2954. NA NA
## 15 Switzerla… arima 4.56e+11 -1322. 2655. 2655. 2667. NA NA
## 16 US arima 4.78e+11 -1311. 2633. 2634. 2648. NA NA
## # … with 3 more variables: MAE <dbl>, ar_roots <list>, ma_roots <list>
Mit der Forecast Funktion erzeugen wir die Prognosen für jede Zeitreihe aus den Modellen.
fc = fit %>%
forecast(h = "2 years")
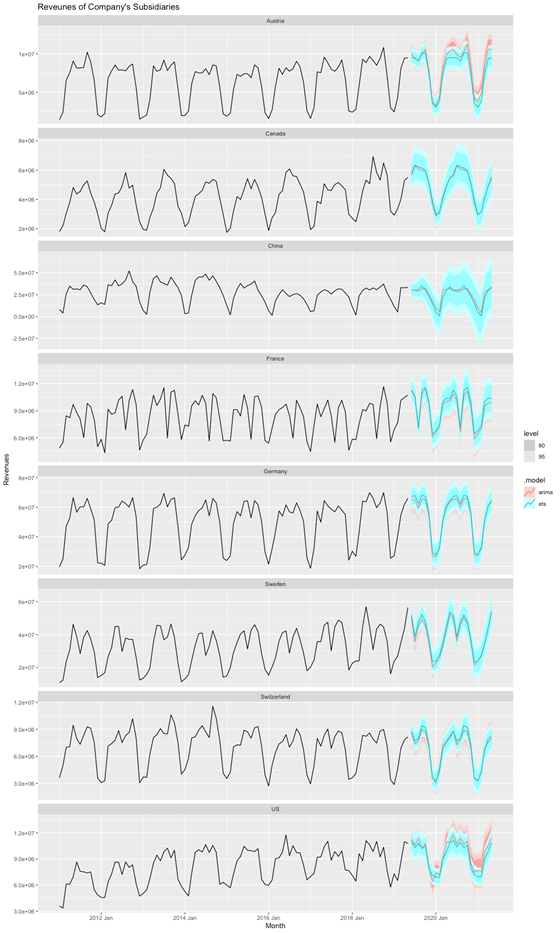
Zum Schluss visualisieren wir die Forecasts. Es ist ersichtlich, dass beide Methoden die Muster der einzelnen Zeitreihen auffangen und in den Forecast ihrer entsprechenden Methodik einarbeiten, wie das z. B. beim „Sommerloch“ in der französischen Tochtergesellschaft oder dem steigenden Trend in der US-Gesellschaft der Fall ist.
fc %>% autoplot(prep_data) +
ggtitle("Reveunes of Company's Subsidiaries")
Wiki-Artikel als PDF herunterladen
Mehr wissen?
Sie möchten tiefer in dieses Thema einsteigen? Dann freuen wir uns, persönlich mit Ihnen über die Anwendungsbereiche von R zu sprechen – gerne auch im Zusammenhang mit Analytics-Produkten der SAP. Nehmen Sie einfach Kontakt mit uns auf!
